پیشتر در وبلاگ فرادرس در مورد اصول و مفاهیم استاتیک صحبت کردیم. در این قسمت قصد داریم تا در مورد مثالهایی بحث کنیم که پایه و اساس سیستمهای استاتیکی پیچیدهتر را تشکیل میدهند.
فیلم آموزش استاتیک به همراه حل مثال — از صفر تا صد (+ دانلود فیلم آموزش گام به گام)
مثال ۱
مطابق شکل زیر میلهای را تصور کنید که توسط دو طناب به صورت معلق نگه داشته شده. جرم و طول این میله را بهترتیب برابر با M و L در نظر بگیرید. طناب اول به فاصله x1 و طناب دوم به فاصله x2 از نقطه A (این نقطه، ابتدای میله است)، میله را نگه داشتهاند.
فرض میشود همواره x1 از x2 بزرگتر است. با فرضیات صورت گرفته، هدف ما محاسبه نیروهای T1 و T2 است. از این رو در قدم اول، بایستی مرکز جرم میله را محاسبه کنیم. از آنجایی که توزیع جرم در این جسم، به صورت یکنواخت در نظر گرفته شده، بنابراین میتوان با انتگرالگیری، مختصات مرکز جرم را محاسبه کرد. البته به یاد داشته باشید که در جسمهای متقارن که توزیع جرم در آنها یکنواخت است، مرکز جرم را بایستی دقیقا مرکز سطح آن در نظر گرفت. برای مثال در این مسئله مرکز جرم در $$x={L \over 2}$$ است.
قدم بعدی بهمنظور حل این مسئله، شناسایی تمامی نیروهایی است که به میله وارد میشوند. لطفا قبل از مطالعه ادامه مطلب تلاش کنید تا نیروهای وارد به میله را شناسایی کنید. در این مسئله با سه نیروی T1 و T2 و Mg مواجه هستیم. تمامی این نیروها در راستای عمودی هستند و هیچ نیروی افقی در مسئله وجود ندارد. پس از شناسایی نیروهای وارد شده به سیستم، زمان آن فرا رسیده تا معادله تعادل آنها را بنویسیم. توجه داشته باشید که به منظور نوشتن معادله تعادل، میتوان نیروهایی که رو به بالا به جسم وارد میشوند را با علامت مثبت و نیروهای رو به پایین را با علامت منفی نشان داد. با این فرض، معادله تعادل نیرو، به شکل زیر است.
$$T_1+T_2-Mg=0$$
اگر توجه کرده باشید در این مسئله با دو مجهول روبرو هستیم؛ از این رو برای یافتن آنها به دو معادله نیاز داریم. به نظر شما معادله بعدی بر چه اساسی نوشته میشود؟ بله درست حدس زدید. معادله دوم، همان تعادل گشتاور نیروهای وارد شده به سیستم است. بنابراین در این قدم، تعادل گشتاور نیروهای وارد شده به میله را مینویسیم. توجه داشته باشید که بهمنظور نوشتن معادله تعادل گشتاور بایستی نقطهای را تعیین کنیم که تعادل مدنظر حول آن نوشته شود. بهترین راه این است که نقطه را به شکلی انتخاب کنیم که بیشترین مجهولات (که در این مسئله دو نیروی T1 و T۲ هستند) کنار روند. در این مسئله، تعادلِ گشتاور را حول نقطه A مینویسیم. بنابراین میتوان گفت:
$$x_1T_1+x_2T_2-{1 \over 2}Mg=0$$
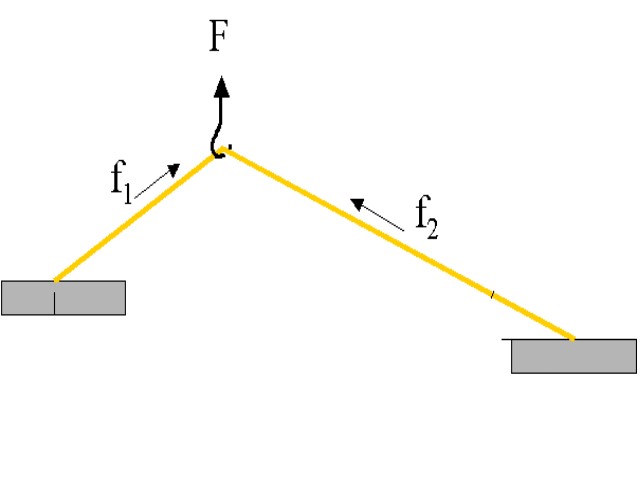
توجه داشته باشید که برای محاسبه گشتاور یک نیرو حول نقطهای خاص، نیروی مذکور را در فاصله آن ضرب میکنیم. شکل زیر گشتاور ناشی از وارد کردن نیروی F به دسته یک آچار را نشان میدهد. این گشتاور حول پیچ محاسبه شده است.
به ادامه مثال ۱ باز میگردیم. بنابراین تاکنون دو معادله تعادل نیرو و گشتاور برای این میله، به صورت زیر بیان شدند.
$$T_1+T_2-Mg=0$$
$$x_1T_1+x_2T_2-{1 \over 2}Mg=0$$
همانطور که میبینید با دو معادله و دو مجهول (T1 و T2) مواجه هستیم. با حل این دو معادله، این نیروها برابر با مقادیر زیر محاسبه میشوند.
مثال ۲
مطابق شکل زیر، میلهای با جرم یکنواختِ M و طول L را تصور کنید که حول نقطهای لولا شده است. سمت دیگر این میله، توسط یک کابل، متصل به دیوار نگه داشته شده. با فرض اینکه میله به صورت افقی قرار گرفته باشد، قصد داریم تا جهت و اندازه نیروهای وارد شده به میله از طرف کابل و لولا را محاسبه کنیم.
مطابق با مفاهیم ارائه شده در مثال ۱، مرکز جرم این میله دقیقا در وسط آن قرار گرفته است. همانطور که پیشتر نیز بیان شد، در قدم اول بایستی تمامی نیروهایی که به میله وارد میشوند را شناسایی کنیم. در این مسئله، ۳ نیرویِ وزن (Mg)، لولا (R) و کابل (T) به سیستم وارد میشوند. برای نوشتن معادله تعادل نیرویی، در ابتدا جهت نیروهای R و T با میله را به ترتیب برابر با $$\phi$$ و $$\theta$$ فرض میکنیم. با این فرض، تعادل نیرو در راستای x را میتوانیم به صورت زیر بنویسیم.
معادله ۱
بر همین مبنا تعادل نیرویی در راستای y را میتوان به شکل زیر نوشت.
معادله ۲
توجه داشته باشید که در حالت کلی، معادلات تعادل نیرویی در تمامی راستاها بایستی نوشته شوند. برای مثال در یک مسئله سهبعدی، تعادل نیرویی را بایستی در راستاهای y ،x و z نوشت.
حال وقت آن رسیده که تعادل گشتاور را بنویسیم. برای اینکه نیروی R از رابطه تعادل گشتاور حذف شود، میتوان معادله را حول لولا نوشت. بنابراین داریم:
معادله ۳
همانطور که در بالا میبینید، عبارت دوم بهصورت منفی ظاهر شده. دلیل این علامت این است که نیروی T، میله را خلاف جهت نیروی وزن میچرخاند. در شکل زیر این جهات برای یک جسم فرضی نشان داده شده اند.
با حل معادلات ۱ و ۲ میتوان نیروهای T و R را بر حسب زاویای $$\phi$$ و $$\theta$$، به صورت زیر بدست آورد.
بالا: معادله ۴. پایین: معادله ۵
با جایگذاری معادله ۴ در معادله ۳ رابطه بین دو زاویه مد نظر به شکل زیر محاسبه میشود.
همانطور که از ریاضیات میدانیم، از این معادله میتوان نتیجه گرفت که زوایای $$\phi$$ و $$\theta$$ با یکدیگر برابر هستند [این نتیجه با توجه به رابطه $$sin 2\theta=2sin \theta \enspace cos\theta$$ حاصل شده]. با بدست آمدن این دو زاویه، جهت دو نیروی T و R نیز مشخص میشوند.
نهایتا با حل معادلات ۴ و ۵ میتوان نیروهای T و R را برابر با مقادیر زیر محاسبه کرد.
نکته جالب مثال بالا در این است که اگر زوایای $$\theta$$ و $$\phi$$ با یکدیگر برابر باشند، میتوان گفت که ۳ نیروی Mg، T و R نیز از یک نقطه (در شکلی که در ابتدای این مثال آمده این نقطه مشخص است) خواهند گذشت.
مثال ۳
تصور کنید که مطابق با شکل زیر دو نوار فلزی در زاویه ۹۰ درجه به یکدیگر جوش داده شدهاند. فرض کنید اطلاعات این دو نوار برابر با مقادیر زیر هستند.
کیلوگرم ۵.۲=m1
کیلوگرم ۳.۴=m۲
متر 1.3=l1
متر ۰.۷=l۲
اگر این مجموعه را رها کنیم، زاویه تعادل نوار l1 و محور عمودی چقدر خواهد بود؟
به منظور حل هر مسئله استاتیکی در ابتدا بایستی دستگاه مختصات مناسب را تعریف کنیم. در این مسئله مبدا دستگاه مختصات را روی لولا فرض میکنیم و محورهای x و y را مطابق با شکل بالا در نظر میگیریم. مرکز جرم نوار شماره ۱ برابر با $$(x_1,y_1)=(0,{L_1 \over 2})$$ است [این مرکز جرم بر اساس دستگاه مختصات، بیان شده]. به همین شکل $$(x_2,y_2)=(0,{L_2 \over 2})$$ را میتوان به عنوان مرکز جرم نوار $$L_2$$ در نظر گرفت. بهمنظور محاسبه مرکز جرم سیستم (نوار ۱ + نوار۲)، از فرمول زیر استفاده میشود.
بر همین مبنا، مختصات y مرکز جرم، به صورت زیر محاسبه میشود.
همانطور که در مثال ۱ نیز بیان شد، هنگامی که سیستمی در یک نقطه لولا شود، مرکز جرم آن بایستی دقیقا در زیر لولا قرار گیرد. بنابراین پس از به تعادل رسیدن، سیستم به شکل زیر در خواهد آمد.
وضعیت مجموعه دو نوار متصل به هم، در حالت تعادل
پس از دوران، زاویه میان بردار مرکز جرم و محور y صفر شده به همان اندازه نوار L1 میچرخد. بنابراین زاویه نوار L1 و محور y در حالت نهایی برابر است با:
مثال ۴
مطابق با شکل زیر دو جرم 36=m1 و 24=m2 توسط میلهای به طول l=3 و جرم m=15 معلق نگه داشته شدهاند. با فرض اینکه زاویه $$\theta$$ برابر با ۴۰ درجه و طول l1 و l2 برابر با ۰.۵ و ۲.۳ باشند، نیروی کشش T را محاسبه کنید.
به نظر شما آیا میتوان تنها با یک معادله نیروی T را یافت؟ در نگاه اول به نظر میرسد پاسخ این سوال منفی باشد چرا که در لولا نیز نیروی مجهول R وجود دارد. اما توجه داشته باشید که با نوشتن گشتاور حول لولا، نیروی R در معادلات ظاهر نخواهد شد. بنابراین گشتاور ایجاد شده توسط نیروها را میتوان حول لولا و به صورت زیر بیان کرد:
با حل این معادله، نیروی T به شکل زیر محاسبه میشود.
در مهندسی عمران و مکانیک از ابزاری تحت عنوان «خرپا» در سازههای مختلف استفاده میشود. این ابزار با تقسیم کردن نیروها در سازه، به آن استحکام میبخشد. در بخش آینده در مورد چگونگی تحلیل نیروهای موجود در یک خرپا صحبت خواهیم کرد.
عمدتا از خرپاها در ساخت پل استفاده میشود.
همچنین در صورت علاقهمندی به مباحث مرتبط در زمینه مکانیک و عمران، احتمالا میتوانید از آموزشهای زیر استفاده کنید:
- مجموعه آموزشی دروس مهندسی مکانیک
- مجموعه آموزشهای دروس مهندسی عمران
- آموزش استاتیک
- اصول استاتیک — به زبان ساده
- آموزش استاتیک (مرور و حل تست کنکور ارشد)
^^
«مجید عوضزاده»، فارغ التحصیل مقطع کارشناسی ارشد رشته مهندسی مکانیک از دانشگاه تهران است. فیزیک، ریاضیات و مهندسی مکانیک از جمله مباحث مورد علاقه او هستند که در رابطه با آنها تولید محتوا میکند.
بر اساس رای 25 نفر
آیا این مطلب برای شما مفید بود؟